Системы счисления

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

• даёт представления множества чисел (целых или вещественных)
• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
• отражает алгебраическую и арифметическую структуру чисел.

Разные народы в разные времена использовали разные системы счисления. Следы древних систем счета встречаются и сегодня в культуре многих народов. К древнему Вавилону восходит деление часа на 60 минут и угла на 360 градусов. К Древнему Риму - традиция записывать в римской записи числа I, II, III и т. д. К англосаксам - счет дюжинами: в году 12 месяцев, в футе 12 дюймов, сутки делятся на 2 периода по 12 часов.

По современным данным, развитые системы нумерации впервые появились в древнем Египте. Для записи чисел египтяне применяли иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и операции сложения. Недостатки этой системы - невозможность записи больших чисел и громоздкость.

В конце концов, самой популярной системой счисления оказалась десятичная система. Десятичная система счисления пришла из Индии, где она появилась не позднее VI в. н. э. В ней всего 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 но информацию несет не только цифра, но также и место позиция, на которой она стоит. В числе 444 три одинаковых цифры обозначают количество и единиц, и десятков, и сотен. А вот в числе 400 первая цифра обозначает число сотен, два 0 сами по себе вклад в число не дают, а нужны лишь для указания позиции цифры 4.

Взаимосвязь между системами счисления с основаниями «2», «8» и «16»

Система счисления (СС) - это система записи чисел с помощью определенного набора цифр. CС называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе. Десятичная СС является позиционной: 999. Римская СС является непозиционной. Значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе. Количество различных цифр, употребляемых в позиционной СС, называется основанием СС. Если основание используемой СС больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение.

В шестнадцатеричной СС основа - это цифры 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 с соответствующими обозначениями 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Примеры чисел: 17D.E, F12A.
Двоичная СС - это система, в которой для записи чисел используются две цифры 0 и 1. Основанием двоичной системы счисления является число 2.Двоичный код числа - запись этого числа в двоичной системе счисления.
Например:
1=1₂
2=10₂
7=111₂
120=1111000₂
В ВТ применяют позиционные СС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную. 16-ричная и 8-ричная СС используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов – команд, данных, адресов и операндов.

Перевод чисел из десятичной СС в заданную.

1) Для перевода целых чисел десятичной системы счисления в другую систему счисления последовательно выполняют деление нацело на основание новой СС, пока не получат частное, меньшее этого основания.. Число в новой СС записывают, начиная с последнего частного, добавляя к нему остатки.
Например: Необходимо перевести число 76 из 10-ной в 2-ую СС.

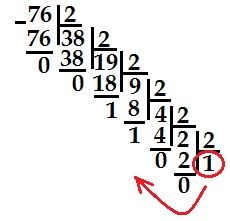
Ответ: 76₁₀=1001100₂.

2) Для перевода десятичных дробей из десятичной СС в другую СС последовательно выполняют умножение дробной части на основание новой системы счисления, пока она не станет равной нулю. Число в новой СС записывают из целых частей произведений, начиная с первого.
Например: Необходимо перевести число 0.35 из 10-ной в 2-ую СС.

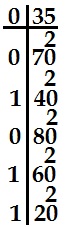
Ответ: 0.35₁₀=0.01011₂

Перевод чисел из произвольной системы в десятичную.

Число записывают в виде суммы произведений цыфр в числе на основание системы счисления в степени порядка. По другому это называется развернутой формой числа.

Например: 1101₂=1^.2₃+1^.2²+0^.2¹+1^.2⁰=13₁₀

17D.E₁₆=1·16²+ 7·16¹+13·16⁰+ 14·16^-1+12·16^-2=381.921875₁₀

Перевод между основаниями, составляющими степень 2.

Для того, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
Например: 234.77₈=010 011 100.111 111₂= 10 011 100.111 111₂
123456₈ = 001 010 011 100 101 110₂= 1 010 011 100 101 110₂

Обратный перевод: двоичное число делят справа налево (целую часть) и слева на право (дробную часть) на триады двоичных цифр. Каждая триада двоичных цифр заменяется восьмеричной цифрой, при этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Например: 1100111₂= 001 100 111₂= 147₈
11.1001₂= 011.100 100₂= 3.44₈

При переводах между двоичной и шестнадцатеричной СС используются четверки цифр. При необходимости выравнивание выполняется до длины двоичного числа, кратной четырем.
Например: 1234.AB77₁₆ = 0001 0010 0011 0100.1010 1011 0111 0111₂1 0010 0011 0100.1010 1011 0111 0111₂
CE567₁₆= 1100 1110 0101 0110 0111₂
1100111₂= 0110 0111₂= 67₁₆

При переходе из восьмеричного счисления в шестнадцатеричное счисление и обратно используется вспомогательный двоичный код числа.
Например: 1234567₈ = 001 010 011 100 101 110 111₂ = 0101 0011 1001 0111 0111₂= 53977₁₆
120.34₈= 001 010 000. 011 100₂= 0101 0000.0111 0000₂= 50.7₁₆
CE4567₁₆= 1100 1110 0100 0101 0110 0111₂= 110 011 100 100 010 101 100 111₂= 63442547₈