Тема 2.1 Тексты и кодирование.
Равномерные и неравномерные коды. Условие Фано.

Тексты и кодирование.

Кодирование — это процесс перевода информации из формы, понятной человеку (текст, изображения, видео и т. д.), в некоторый код.
Декодирование — это процесс перевода информации из кода в форму, понятную человеку.
Код — это условные знаки для представления информации.
Вся информация в компьютере хранится в двоичном коде. Поэтому надо научиться преобразовывать символы в двоичный код.
Формула Хартли определяет количество информации в зависимости от количества возможных вариантов
N=2ⁱ, где p
N — это количество вариантов,
i — это количество бит, не обходимых для кодирования.

Если же мы преобразуем эту формулу и примем за N — количество символов в используемом алфавите (назовем это мощностью алфавита), то мы поймем, сколько памяти потребуется для кодирования одного символа.

N=2ⁱ, где N — кол-во возможных вариантов
i — кол-во бит, потребуемых для кодирования
Итак, если в нашем алфавите будет присутствовать только 32 символа, то каждый из них займет только 5 бит.
N=32 ⇒ i= 5 бит
И тогда каждому символу мы дадим уникальный двоичный код. Такую таблицу мы будем назвать кодировочной

N=32 ⇒ i= 5 бит

Таблица ASCII (американский системный код для обмена информацией) — это стандарт кодирования символов, используемый в компьютерах и других устройствах для текстовых файлов. ASCII — это подмножество Unicode с набором символов из 128 символов. Символы включают заглавные и строчные буквы, цифры, знаки препинания, запоминающиеся символы и управляющие символы. Каждый символ в наборе символов имеет одинаковое шестнадцатеричное и восьмеричное значение, а также десятичное значение в диапазоне от 0 до 127.

ASCII - это стандарт кодировки символов для электронной связи. Текст представлен с помощью кода ASCII в компьютерах, телекоммуникационном оборудовании и других устройствах. Хотя они позволяют использовать гораздо больше символов, большинство современных методов кодирования символов основаны на ASCII.

Управление по присвоению номеров Интернета (IANA) поддерживает обозначение US-ASCII для этой кодировки символов. Одной из вех IEEE является ASCII.

Dec	Hex	Char	Dec	Hex	Char	Dec	Hex	Char	Dec	Hex	Char
0	0	NUL	32	20	(sp)	64	40	@	96	60	`
1	1	SOH	33	21	!	65	41	A	97	61	a
2	2	STX	34	22	"	66	42	B	98	62	b
3	3	ETX	35	23	#	67	43	C	99	63	c
4	4	EOT	36	24	$	68	44	D	100	64	d
5	5	ENQ	37	25	%	69	45	E	101	65	e
6	6	ACK	38	26	&	70	46	F	102	66	f
7	7	BEL	39	27	'	71	47	G	103	67	g
8	8	BS	40	28	(	72	48	H	104	68	h
9	9	TAB	41	29	)	73	49	I	105	69	i
10	A	LF	42	2A	*	74	4A	J	106	6A	j
11	B	VT	43	2B	+	75	4B	K	107	6B	k
12	C	FF	44	2C	,	76	4C	L	108	6C	l
13	D	CR	45	2D	-	77	4D	M	109	6D	m
14	E	SO	46	2E	.	78	4E	N	110	6E	n
15	F	SI	47	2F	/	79	4F	O	111	6F	o
16	10	DLE	48	30	0	80	50	P	112	70	p
17	11	DC1	49	31	1	81	51	Q	113	71	q
18	12	DC2	50	32	2	82	52	R	114	72	r
19	13	DC3	51	33	3	83	53	S	115	73	s
20	14	DC4	52	34	4	84	54	T	116	74	t
21	15	NAK	53	35	5	85	55	U	117	75	u
22	16	SYN	54	36	6	86	56	V	118	76	v
23	17	ETB	55	37	7	87	57	W	119	77	w
24	18	CAN	56	38	8	88	58	X	120	78	x
25	19	EM	57	39	9	89	59	Y	121	79	y
26	1A	SUB	58	3A	:	90	5A	Z	122	7A	z
27	1B	ESC	59	3B	;	91	5B	[	123	7B	{
28	1C	FS	60	3C	<	92	5C	\	124	7C	\|
29	1D	GS	61	3D	=	93	5D	]	125	7D	}
30	1E	RS	62	3E	>	94	5E	^	126	7E	~
31	1F	US	63	3F	?	95	5F	_	127	7F	DEL

Таблица ASCII была создана под контролем Американской ассоциации стандартов (ASA). То Американская Ассоциация стандартов (ASA) превратилась в США Американского института стандартов (USASI) и, в конечном итоге, Американская Национальный институт стандартов (ANSI).

Для дополнительный После заполнения специальных символов и управляющих кодов ASCII был опубликован как ASA X3.4-1963, оставив 28 кодовых позиций без присвоенного значения и один неназначенный управляющий код. Был существенный спор о том, следует ли использовать дополнительные управляющие символы вместо строчного алфавита. Колебания длились недолго: в мае 1963 года рабочая группа CCITT по новому телеграфному алфавиту выступила за присвоение строчных букв стержням 6 и 7, а в октябре Международная организация по стандартизации TC 97 SC 2 решила включить корректировку в свои проект стандарта

На собрании в мае 1963 года рабочая группа X3.2.4 одобрила переход на ASCII. Расположение строчных букв на палочках 6 и 7 привело к тому, что битовые шаблоны символов отклонились от верхнего регистра на один бит, что упростило сопоставление символов без учета регистра и дизайн клавиатур и принтеров.

Другие модификации, внесенные комитетом X3, включали добавление новых символов (скобки и вертикальные черты), переименование некоторых управляющих символов (SOM стало началом заголовка (SOH)), а также перемещение или удаление других (RU был удален). В результате ASCII был изменен как USAS X3.4-1967, затем USAS X3.4-1968, ANSI X3.4-1977 и, наконец, ANSI X3.4-1986.

Равномерные и неравномерные коды.

Кодирование символов обычно предполагает, что каждому символу всегда сопоставляется одинаковое количество битов (например, в кодовой таблице ASCII каждому символу сопоставляется один байт, хранящий порядковый номер того или иного символа в этой таблице). Такой способ кодирования прост и удобен, однако очевидно, что он является не самым оптимальным. Для значительной части символов используются не все биты отведенных под них байтов (часть старших битов — нулевые), а при наличии в тексте только части символов, предусмотренных в таблице ASCII (например, если текст содержит только прописные русские буквы), приходится все равно использовать 8-битный код.

Более компактным является неравномерный двоичный код (особенно если при его построении исходить из частоты встречаемости различных символов и присваивать наиболее часто используемым знакам самые короткие коды, как это сделано в методе Хаффмана). При этом количество битов, отводимых для кодирования символов, в целом зависит от количества используемых в конкретном случае различных символов (от мощности алфавита), а коды, соответствующие разным символам, могут иметь различную длину в битах.

Главное при таком кодировании — обеспечить возможность однозначного декодирования записанной с помощью этих кодов строки (поочередного, слева направо, выделения и распознавания из сплошной последовательности нулей и единиц кодов отдельных букв). Для этого коды символам необходимо назначать в соответствии с условиями Фано.

Прямое условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо другого, более длинного кода.

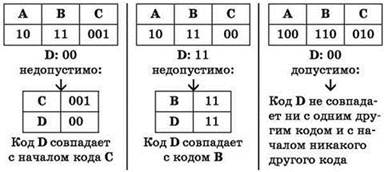
Обратное условие Фано. Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с окончанием (постфиксом) какого-либо другого, более длинного кода.

Для однозначности декодирования последовательности кодов достаточно выполнения хотя бы одного из двух вышеуказанных условий Фано:

при выполнении прямого условия Фано последовательность кодов однозначно декодируется с начала;
при выполнении обратного условия Фано последовательность кодов однозначно декодируется с конца.

Выбрать, какое из двух правил Фано используется при решении конкретной задачи, можно, проанализировав коды в условии задачи (без учёта кода, проверяемого в вариантах ответа): если для исходных кодов выполняется прямое правило Фано, то его и нужно использовать при решении, и наоборот. Вместе с тем нужно помнить, что правила Фано — это достаточное, но не необходимое условие однозначного декодирования: если не выполняется ни прямое, ни обратное правило Фано, конкретная двоичная последовательность может оказаться такой, что она декодируется однозначно (так как остальные возможные варианты до конца декодирования довести не удаётся). В подобном случае необходимо пытаться строить дерево декодирования в обоих направлениях.

Рекомендуется начинать решение задач такого типа с анализа выполнимости правил Фано для исходных кодов, указанных в условии задачи (т.е. без учета искомого кода в вариантах ответов). В зависимости от того, какое из двух правил Фано выполняется для исходных кодов, при дальнейшем решении задачи производится сравнение более короткого кода с началом (при выполнении прямого правила Фано) или с концом (при выполнении обратного правила Фано) более длинного кода.

Если для заданной последовательности кодов выполняется прямое правило Фано, то её декодирование необходимо вести с начала (слева направо).

Если для заданной последовательности кодов выполняется обратное правило Фано, то её декодирование необходимо вести с конца (справа налево).

При сравнении пары кодов удобно подписывать более короткий код под более длинным, выравнивая эти записи по левому краю — для прямого правила Фано либо по правому краю — для обратного правила Фано.

Тема 2.1 Тексты и кодирование. Равномерные и неравномерные коды. Условие Фано.

Тексты и кодирование.

Равномерные и неравномерные коды.

Тема 2.1 Тексты и кодирование.
Равномерные и неравномерные коды. Условие Фано.