Математические основы информатики.
Основные определения информатики.
Математические основы информатики — сочетание слов странное, с какой стороны на него ни посмотри.
Если это про применение математических методов в информатике — а об этом, безусловно, предстоит вести речь,
— то почему нет, например, математических основ физики или химии, где математика весьма изощренно используется уже столетия?
Если о том, что информатика как научная теория своим происхождением и развитием обязана математике, то, как повзрослевшее дитя,
она давно уже выпорхнула из родового гнездышка, обзавелась пестрым оперением информационных технологий — и стоит ли поминать в этой ситуации старушку-мать,
т.е. математику. Современное определение информатики как науки, изучающей информационные процессы в природе, технике и обществе,
вообще не содержит и намека на какую-то связь с математикой.
Разберемся по порядку. Основные информационные процессы, как известно, — это получение, хранение, передача и обработка информации.
Именно их изучение и представляет собой основную цель информатики. Надо только еще сказать, что акцент делается на автоматизации этих процессов.
Не случайно бытует мнение, что сам термин ИНФОРМАТИКА происходит от соединения слов ИНФОРмация и автоМАТИКА.
Без указанного акцента информатика неизбежно становится сборищем фрагментов других научных дисциплин: семиотики, изучающей знаковые системы, лингвистики,
изучающей закономерности языка как средства передачи информации, психологии, изучающей, в частности, процессы обработки информации человеком,
этологии, изучающей поведение животных, архивоведения, формулирующего правила хранения информации, библиологии, занимающейся организацией хранения и поиска информации, и т.д.
Система счисления— это совокупность приемов и правил, по которым числа записываются и читаются.
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах счислениявес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа.
Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
В позиционных системах счислениявес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр,
изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Сама же запись числа 757,7 означает сокращенную запись выражения
700 + 50 + 7 + 0,7 = 7 . 102+ 5 . 101+ 7 . 100+ 7 . 10—1= 757,7.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления— количество различных цифр, используемых для изображения чисел в данной системе счисления.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д.
Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.
Запись чисел в каждой из систем счисления с основаниемqозначает сокращенную запись выражения
an-1 qn-1 + an-2 qn-2 + ... + a1 q1 + a0 q0 + a-1 q-1 + ... + a-m q-m,
где ai—
цифры системы счисления; n и m — число целых и дробных
разрядов, соответственно.
Например:
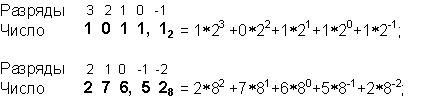
Целые числа в позиционных системах счисления.
В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.
Продвижением цифры называют замену её следующей по величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть цифру 2 значит заменить её на 3 и т.д.
Продвижение старшей цифры(например, цифры 9 в десятичной системе) означает замену её на 0.
В двоичной системе, использующей только две цифры — 0 и 1, продвижение 0 означает замену его на 1, а продвижение 1 — замену её на 0.
Целые числа в любой системе счисления порождаются с помощью Правила счета:
Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа;
если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.
Применяя это правило, запишем первые десять целых чисел
в двоичной системе: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
в троичной системе: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
в пятеричной системе: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
в восьмеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
двоичная (используются цифры 0, 1);
восьмеричная (используются цифры 0, 1, ..., 7);
шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9,
а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:
| 10-я | 2-я | 8-я | 16-я |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |